Chapter 4 Probability
4.1 Student Learning Objective
This section extends the notion of variability that was introduced in the context of data to other situations. The variability of the entire population and the concept of a random variable is discussed. These concepts are central for the development and interpretation of statistical inference. By the end of the chapter the student should:
Consider the distribution of a variable in a population and compute parameters of this distribution, such as the mean and the standard deviation.
Become familiar with the concept of a random variable.
Understand the relation between the distribution of the population and the distribution of a random variable produced by sampling a random subject from the population.
Identify the distribution of the random variable in simple settings and compute its expectation and variance.
4.2 Different Forms of Variability
In the previous chapters we examined the variability in data. In the statistical context, data is obtained by selecting a sample from the target population and measuring the quantities of interest for the subjects that belong to the sample. Different subjects in the sample may obtain different values for the measurement, leading to variability in the data.
This variability may be summarized with the aid of a frequency table, a table of relative frequency, or via the cumulative relative frequency. A graphical display of the variability in the data may be obtained with the aid of the bar plot, the histogram, or the box plot.
Numerical summaries may be computed in order to characterize the main features of the variability. We used the mean and the median in order to identify the location of the distribution. The sample variance, or better yet the sample standard deviation, as well as the inter-quartile range were all described as tools to quantify the overall spread of the data.
The aim of all these graphical representations and numerical summaries is to investigate the variability of the data.
The subject of this chapter is to introduce two other forms of variability, variability that is not associated, at least not directly, with the data that we observe. The first type of variability is the population variability. The other type of variability is the variability of a random variable.
The notions of variability that will be presented are abstract, they are not given in terms of the data that we observe, and they have a mathematical-theoretical flavor to them. At first, these abstract notions may look to you as a waste of your time and may seem to be unrelated to the subject matter of the course. The opposite is true. The very core of statistical thinking is relating observed data to theoretical and abstract models of a phenomena. Via this comparison, and using the tools of statistical inference that are presented in the second half of the book, statisticians can extrapolate insights or make statements regarding the phenomena on the basis of the observed data. Thereby, the abstract notions of variability that are introduced in this chapter, and are extended in the subsequent chapters up to the end of this part of the book, are the essential foundations for the practice of statistics.
The first notion of variability is the variability that is associated with the population. It is similar in its nature to the variability of the data. The difference between these two types of variability is that the former corresponds to the variability of the quantity of interest across all members of the population and not only for those that were selected to the sample.
In Chapters 2 and 3 we examined the data
set “ex.1” which contained data on the sex and height of a sample of
100 observations. In this chapter we will consider the sex and height of
all the members of the population from which the sample was selected.
The size of the relevant population is 100,000, including the 100
subjects that composed the sample. When we examine the values of the
height across the entire population we can see that different people may
have different heights. This variability of the heights is the
population variability.
The other abstract type of variability, the variability of a random variable, is a mathematical concept. The aim of this concept is to model the notion of randomness in measurements or the uncertainty regarding the outcome of a measurement. In particular we will initially consider the variability of a random variable in the context of selecting one subject at random from the population.
Imagine we have a population of size 100,000 and we are about to select at random one subject from this population. We intend to measure the height of the subject that will be selected. Prior to the selection and measurement we are not certain what value of height will be obtained. One may associate the notion of variability with uncertainty — different subjects to be selected may obtain different evaluations of the measurement and we do not know before hand which subject will be selected. The resulting variability is the variability of a random variable.
Random variables can be defined for more abstract settings. Their aim is to provide models for randomness and uncertainty in measurements. Simple examples of such abstract random variables will be provided in this chapter. More examples will be introduced in the subsequent chapters. The more abstract examples of random variables need not be associated with a specific population. Still, the same definitions that are used for the example of a random variable that emerges as a result of sampling a single subject from a population will apply to the more abstract constructions.
All types of variability, the variability of the data we dealt with before as well as the other two types of variability, can be displayed using graphical tools and characterized with numerical summaries. Essentially the same type of plots and numerical summaries, possibly with some modifications, may and will be applied.
A point to remember is that the variability of the data relates to a concrete list of data values that is presented to us. In contrary to the case of the variability of the data, the other types of variability are not associated with quantities we actually get to observe. The data for the sample we get to see but not the data for the rest of the population. Yet, we can still discuss the variability of a population that is out there, even though we do not observe the list of measurements for the entire population. (The example that we give in this chapter of a population was artificially constructed and serves for illustration only. In the actual statistical context one does not obtain measurements from the entire population, only from the subjects that went into the sample.) The discussion of the variability in this context is theoretical in its nature. Still, this theoretical discussion is instrumental for understanding statistics.
4.3 A Population
In this section we introduce the variability of a population and present some numerical summaries that characterizes this variability. Before doing so, let us review with the aid of an example some of the numerical summaries that were used for the characterization of the variability of data.
Recall the file “ex1.csv” that contains data on the height and sex of
100 subjects. (The data file can be obtained from
http://pluto.huji.ac.il/~msby/StatThink/Datasets/ex1.csv.) We read the
content of the file into a data frame by the name “ex.1” and apply the
function “summary” to the data frame:
ex.1 <- read.csv("_data/ex1.csv")
summary(ex.1)## id sex height
## Min. :1538611 FEMALE:54 Min. :117.0
## 1st Qu.:3339583 MALE :46 1st Qu.:158.0
## Median :5105620 Median :171.0
## Mean :5412367 Mean :170.1
## 3rd Qu.:7622236 3rd Qu.:180.2
## Max. :9878130 Max. :208.0We saw in the previous chapter that, when applied to a numeric sequence,
the function “summary” produces the smallest and largest values in the
sequence, the three quartiles (including the median) and the mean. If
the input of the same function is a factor then the outcome is the
frequency in the data of each of the levels of the factor. Here “sex”
is a factor with two levels. From the summary we can see that 54 of the
subjects in the sample are female and 46 are male.
Notice that when the input to the function “summary” is a data frame,
as is the case in this example, then the output is a summary of each of
the variables of the data frame. In this example two of the variables
are numeric (“id” and “height”) and one variable is a factor
(“sex”).
Recall that the mean is the arithmetic average of the data which is computed by summing all the values of the variable and dividing the result by the number of observations. Hence, if \(n\) is the number of observations (\(n=100\) in this example) and \(x_i\) is the value of the variable for subject \(i\), then one may write the mean in a formula form as
\[\bar x = \frac{\mbox{Sum of all values in the data}}{\mbox{Number of values in the data}} = \frac{\sum_{i=1}^n x_i}{n}\;,\]
where \(\bar x\) corresponds to the mean of the data and the symbol “\(\sum_{i=1}^n x_i\)” corresponds to the sum of all values in the data.
The median is computed by ordering the data values and selecting a value that splits the ordered data into two equal parts. The first and third quartile are obtained by further splitting each of the halves into two quarters.
Let us discuss the variability associated with an entire target
population. The file “pop1.csv” that contains the population data can
be found on the internet
(http://pluto.huji.ac.il/~msby/StatThink/Datasets/pop1.csv). It is a
CSV file that contains the information on sex and height of an entire
adult population of some imaginary city. (The data in “ex.1”
corresponds to a sample from this city.) Read the population data into
R and examine it:
pop.1 <- read.csv(file="_data/pop1.csv")
summary(pop.1)## id sex height
## Min. :1000082 FEMALE:48888 Min. :117
## 1st Qu.:3254220 MALE :51112 1st Qu.:162
## Median :5502618 Median :170
## Mean :5502428 Mean :170
## 3rd Qu.:7757518 3rd Qu.:178
## Max. :9999937 Max. :217The object “pop.1” is a data frame of the same structure as the data
frame “ex.1”. It contains three variables: a unique identifier of each
subject (id), the sex of the subject (sex), and its height
(height). Applying the function “summary” to the data frame produces
the summary of the variables that it contains. In particular, for the
variable “sex”, which is a factor, it produces the frequency of its
two categories – 48,888 female and 51,112 – a total of 100,000 subjects.
For the variable “height”, which is a numeric variable, it produces
the extreme values, the quartiles, and the mean.
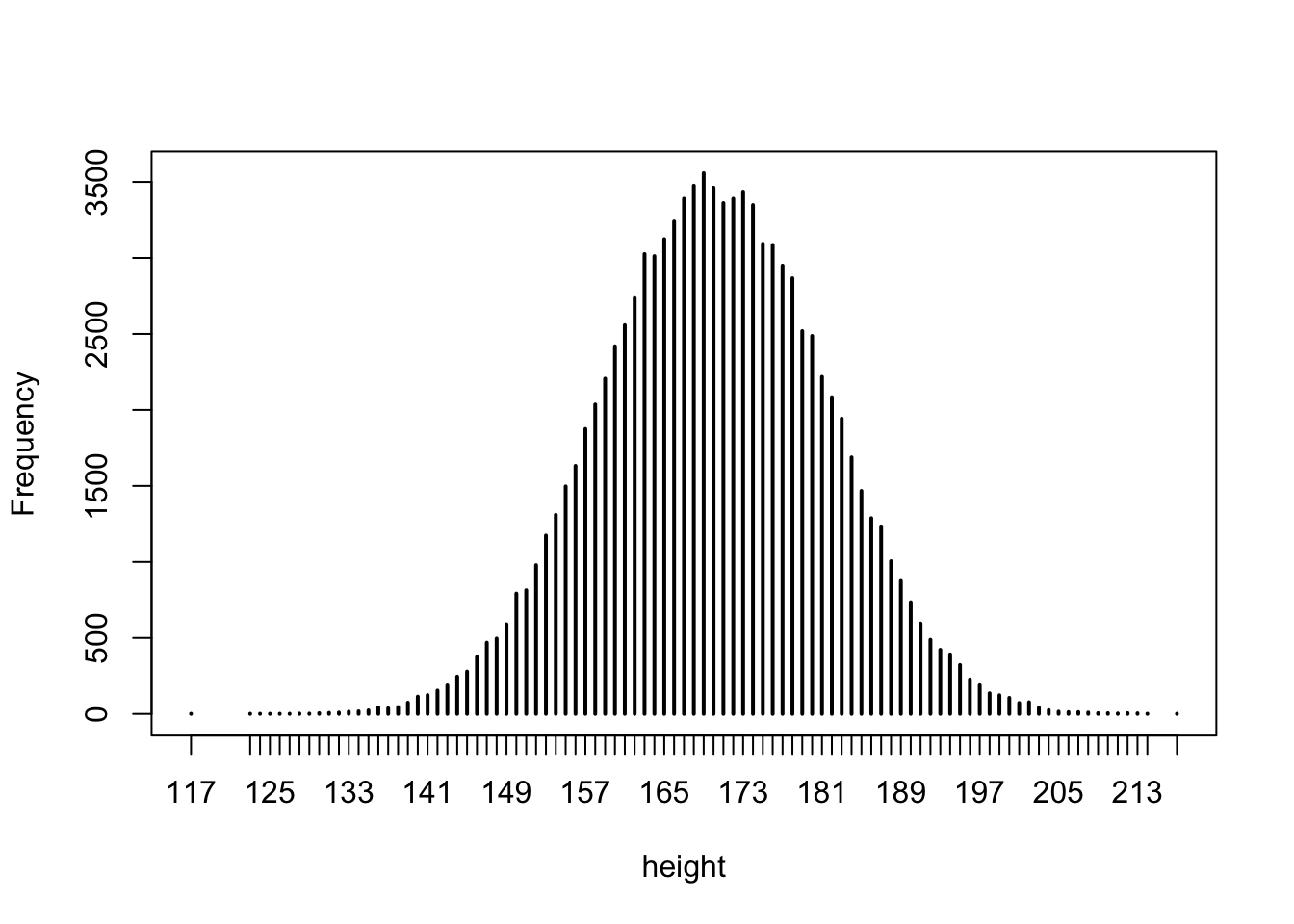
FIGURE 4.1: Bar Plot of Height
Let us concentrate on the variable “height”. A bar plot of the
distribution of the heights in the entire population is given in
Figure 4.1 6. Recall that a vertical bar is placed
above each value of height that appears in the population, with the
height of the bar representing the frequency of the value in the
population. One may read out of the graph or obtain from the numerical
summaries that the variable takes integer values in the range between
117 and 217 (heights are rounded to the nearest centimeter). The
distribution is centered at 170 centimeter, with the central 50% of the
values spreading between 162 and 178 centimeters.
The mean of the height in the entire population is equal to 170 centimeter. This mean, just like the mean for the distribution of data, is obtained by the summation of all the heights in the population divided by the population size. Let us denote the size of the entire population by \(N\). In this example \(N = 100,000\). (The size of the sample for the data was called \(n\) and was equal to \(n=100\) in the parallel example that deals with the data of a sample.) The mean of an entire population is denoted by the Greek letter \(\mu\) and is read “mew”. (The average for the data was denoted \(\bar x\)). The formula of the population mean is:
\[\mu = \frac{\mbox{Sum of all values in the population}}{\mbox{Number of values in the population}}= \frac{\sum_{i=1}^N x_i}{N}\;.\]
Observe the similarity between the definition of the mean for the data and the definition of the mean for the population. In both cases the arithmetic average is computed. The only difference is that in the case of the mean of the data the computation is with respect to the values that appear in the sample whereas for the population all the values in the population participate in the computation.
In actual life, we will not have all the values of a variable in the entire population. Hence, we will not be able to compute the actual value of the population mean. However, it is still meaningful to talk about the population mean because this number exists, even though we do not know what its value is. As a matter of fact, one of the issues in statistics is to try to estimate this unknown quantity on the basis of the data we do have in the sample.
A characteristic of the distribution of an entire population is called a parameter. Hence, \(\mu\), the population average, is a parameter. Other examples of parameters are the population median and the population quartiles. These parameters are defined exactly like their data counterparts, but with respect to the values of the entire population instead of the observations in the sample alone.
Another example of a parameter is the population variance. Recall that the sample variance was defined with the aid of the deviations \(x_i - \bar x\), where \(x_i\) is the value of the measurement for the \(i\)th subject and \(\bar x\) is the mean for the data. In order to compute the sample variance these deviations were squared to produce the squared deviations. The squares were summed up and then divided by the sample size minus one (\(n-1\)). The sample variance, computed from the data, was denoted \(s^2\).
The population variance is defined in a similar way. First, the deviations from the population mean \(x_i - \mu\) are considered for each of the members of the population. These deviations are squared and the average of the squares is computed. We denote this parameter by \(\sigma^2\) (read “sigma square”). A minor difference between the sample variance and the population variance is that for the latter we should divide the sum of squared deviations by the population size (\(N\)) and not by the population size minus one (\(N-1\)):
\[\begin{aligned} \sigma^2 =& \mbox{The average square deviation in the population}\\ =& \frac{\mbox{Sum of the squares of the deviations in the population}}{\mbox{Number of values in the population}}\\ =& \frac{\sum_{i=1}^N (x_i-\mu)^2}{N}\;.\end{aligned}\]
The standard deviation of the population, yet another parameter, is denoted by \(\sigma\) and is equal to the square root of the variance. The standard deviation summarizes the overall variability of the measurement across the population. Again, the typical situation is that we do not know what the actual value of the standard deviation of the population is. Yet, we may refer to it as a quantity and we may try to estimate its value based on the data we do have from the sample.
For the height of the subjects in our imaginary city we get that the
variance is equal to \(\sigma^2 =126.1576\). The standard deviation is
equal to \(\sigma = \sqrt{126.1576} = 11.23199\). These quantities can be
computed in this example from the data frame “pop.1” with the aid of
the functions “var” and “sd”, respectively7.
4.4 Random Variables
In the previous section we dealt with the variability of the population. Next we consider the variability of a random variable. As an example, consider taking a sample of size \(n=1\) from the population (a single person) and measuring his/her height.
The object pop.1$height is a sequence with 100,000 entries. Think of
it as a population. We will apply the function “sample” to this
sequence:
sample(pop.1$height,1)## [1] 177The first entry to the function is the given sequence of heights. When we set the second argument to 1 then the function selects one of the entries of the sequence at random, with each entry having the same likelihood of being selected. Specifically, in this example an entry that contains the value 162 was selected. Let us run the function again:
sample(pop.1$height,1)## [1] 168In this instance an entry with a different value was selected. Try to run the command several times yourself and see what you get. Would you necessarily obtain a different value in each run?
Now let us enter the same command without pressing the return key:
sample(pop.1$height,1)Can you tell, before pressing the key, what value will you get?
The answer to this question is of course “No”. There are 100,000 entries with a total of 94 distinct values. In principle, any of the values may be selected and there is no way of telling in advance which of the values will turn out as an outcome.
A random variable is the future outcome of a measurement, before the measurement is taken. It does not have a specific value, but rather a collection of potential values with a distribution over these values. After the measurement is taken and the specific value is revealed then the random variable ceases to be a random variable! Instead, it becomes data.
Although one is not able to say what the outcome of a random variable will turn out to be. Still, one may identify patterns in this potential outcome. For example, knowing that the distribution of heights in the population ranges between 117 and 217 centimeter one may say in advance that the outcome of the measurement must also be in that interval. Moreover, since there is a total of 3,476 subjects with height equal to 168 centimeter and since the likelihood of each subject to be selected is equal then the likelihood of selecting a subject of this height is 3,476/100,000 = 0.03476. In the context of random variables we call this likelihood probability. In the same vain, the frequency of subjects with hight 192 centimeter is 488, and therefore the probability of measuring such a height is 0.00488. The frequency of subjects with height 200 centimeter or above is 393, hence the probability of obtaining a measurement in the range between 200 and 217 centimeter is 0.00393.
4.4.1 Sample Space and Distribution
Let us turn to the formal definition of a random variable: A random variable refer to numerical values, typically the outcome of an observation, a measurement, or a function thereof.
A random variable is characterized via the collection of potential values it may obtain, known as the sample space and the likelihood of obtaining each of the values in the sample space (namely, the probability of the value). In the given example, the sample space contains the 94 integer values that are marked in Figure 4.1. The probability of each value is the height of the bar above the value, divided by the total frequency of 100,000 (namely, the relative frequency in the population).
We will denote random variables with capital Latin letters such as \(X\), \(Y\), and \(Z\). Values they may obtain will be marked by small Latin letters such as \(x\), \(y\), \(z\). For the probability of values we will use the letter “\(\Prob\)”. Hence, if we denote by \(X\) the measurement of height of a random individual that is sampled from the given population then:
\[\Prob(X = 168) = 0.03476\] and \[\Prob(X \geq 200) = 0.00393\;.\]
Consider, as yet another example, the probability that the height of a random person sampled from the population differs from 170 centimeter by no more than 10 centimeters. (In other words, that the height is between 160 and 180 centimeters.) Denote by \(X\) the height of that random person. We are interested in the probability \(\Prob(|X -170| \leq 10)\).8
The random person can be any of the subjects of the population with equal probability. Thus, the sequence of the heights of the 100,000 subjects represents the distribution of the random variable \(X\):
pop.1 <- read.csv(file="_data/pop1.csv")
X <- pop.1$heightNotice that the object “X” is a sequence of lenght 100,000 that stores
all the heights of the population. The probability we seek is the
relative frequency in this sequency of values between 160 and 180. First
we compute the probability and then explain the method of computation:
mean(abs(X-170) <= 10)## [1] 0.64541We get that the height of a person randomly sampled from the population is between 160 and 180 centimeters with probability 0.64541.
Let us produce a small example that will help us explain the computation of the probability. We start by forming a sequence with 10 numbers:
Y <- c(6.3, 6.9, 6.6, 3.4, 5.5, 4.3, 6.5, 4.7, 6.1, 5.3)The goal is to compute the proportion of numbers that are in the range \([4,6]\) (or, equivalently, \(\{|Y-5| \leq 1\}\)).
The function “abs” computes the absolute number of its input argument.
When the function is applied to the sequence “Y-5” it produces a
sequence of the same length with the distances between the components of
“Y” and the number 5:
abs(Y-5)## [1] 1.3 1.9 1.6 1.6 0.5 0.7 1.5 0.3 1.1 0.3Compare the resulting output to the original sequence. The first value in the input sequence is 6.3. Its distance from 5 is indeed 1.3. The fourth value in the input sequence is 3.4. The difference 3.4 - 5 is equal to -1.6, and when the absolute value is taken we get a distance of 1.6.
The function “<=” expects an argument to the right and an argument to
the left. It compares each component to the left with the parallel
component to the right and returns a logical value, “TRUE” or
“FALSE”, depending on whether the relation that is tested holds or
not:
abs(Y - 5) <= 1## [1] FALSE FALSE FALSE FALSE TRUE TRUE FALSE TRUE FALSE TRUEObserve the in this example the function “<=” produced 10 logical
values, one for each of the elements of the sequence to the left of it.
The first input in the sequence “Y” is 6.3, which is more than one
unit away from 5. Hence, the first output of the logical expression is
“FALSE”. On the other hand, the last input in the sequence “Y” is
5.3, which is within the range. Therefore, the last output of the
logical expression is “TRUE”.
Next, we compute the proportion of “TRUE” values in the sequence:
mean(abs(Y - 5) <= 1)## [1] 0.4When a sequence with logical values is entered into the function
“mean” then the function replaces the TRUE’s by 1 and the FALSE’s
by 0. The average produces then the relative frequency of TRUE’s in
the sequence as required. Specifically, in this example there are 4
TRUE’s and 6 FALSE’s. Consequently, the output of the final
expression is \(4/10 = 0.4\).
The computation of the probability that the sampled height falls within
10 centimeter of 170 is based on the same code. The only differences are
that the input sequence “Y” is replaced by the sequence of population
heights “X” as input. the number “5” is replaced by the number
“170” and the number “1” is replaced by the number “10”. In both
cases the result of the computation is the relative proportion of the
times that the values of the input sequence fall within a given range of
the indicated number.
The probability function of a random variable is defined for any value that the random variable may obtain and produces the distribution of the random variable. The probability function may emerge as a relative frequency as in the given example or it may be a result of theoretical modeling. Examples of theoretical random variables are presented mainly in the next two chapters.
Consider an example of a random variable. The sample space and the probability function specify the distribution of the random variable. For example, assume it is known that a random variable \(X\) may obtain the values 0, 1, 2, or 3. Moreover, imagine that it is known that \(\Prob(X=1) = 0.25\), \(\Prob(X=2) = 0.15\), and \(\Prob(X=3)= 0.10\). What is \(\Prob(X=0)\), the probability that \(X\) is equal to 0?
The sample space, the collection of possible values that the random variable may obtain is the collection \(\{0,1,2,3\}\). Observe that the sum over the positive values is:
\[\Prob(X > 0) = \Prob(X=1) + \Prob(X=2) + \Prob(X=3) = 0.25 + 0.15 + 0.10 = 0.50\;.\] It follows, since the sum of probabilities over the entire sample space is equal to 1, that \(\Prob(X=0) = 1- 0.5 = 0.5\).
| Value | Probability | Cum.Prob |
|---|---|---|
| 0 | 0.50 | 0.50 |
| 1 | 0.25 | 0.75 |
| 2 | 0.15 | 0.90 |
| 3 | 0.10 | 1.00 |
Table 4.1 summarizes the distribution of the random variable \(X\). Observe the similarity between the probability function and the notion of relative frequency that was discussed in Chapter 2. Both quantities describe distribution. Both are non-negative and sum to 1. Likewise, notice that one may define the cumulative probability the same way cumulative relative frequency is defined: Ordering the values of the random variable from smallest to largest, the cumulative probability at a given value is the sum of probabilities for values less or equal to the given value.
Knowledge of the probabilities of a random variable (or the cumulative probabilities) enables the computation of other probabilities that are associated with the random variable. For example, considering the random variable \(X\) of Table 4.1, we may calculate the probability of \(X\) falling in the interval \([0.5, 2.3]\). Observe that the given range contains two values from the sample space, 1 and 2, therefore:
\[\Prob(0.5 \leq X \leq 2.3) = \Prob(X=1) + \Prob(X = 2) = 0.25 + 0.15 = 0.40\;.\] Likewise, we may produce the probability of \(X\) obtaining an odd value:
\[\Prob(X = \mbox{odd}) = \Prob(X=1) + \Prob(X=3) = 0.25 + 0.10 = 0.35\;.\] Observe that both \(\{0.5 \leq X \leq 2.3\}\) and \(\{X = \mbox{odd}\}\) refer to subsets of values of the sample space. Such subsets are denoted events. In both examples the probability of the event was computed by the summation of the probabilities associated with values that belong to the event.
4.4.2 Expectation and Standard Deviation
We may characterize the center of the distribution of a random variable and the spread of the distribution in ways similar to those used for the characterization of the distribution of data and the distribution of a population.
The expectation marks the center of the distribution of a random variable. It is equivalent to the data average \(\bar x\) and the population average \(\mu\), which was used in order to mark the location of the distribution of the data and the population, respectively.
Recall from Chapter 3 that the average of the data can be computed as the weighted average of the values that are present in the data, with weights given by the relative frequency. Specifically, we saw for the data
\[1,\; 1,\; 1,\; 2,\; 2,\; 3,\; 4,\; 4,\; 4,\; 4,\; 4\] that
\[\frac{1 + 1 + 1 + 2 + 2 + 3 + 4 + 4 + 4 + 4 + 4}{11} = 1\times \frac{3}{11} + 2 \times \frac{2}{11} + 3 \times \frac{1}{11} + 4 \times \frac{5}{11}\;,\] producing the value of \(\bar x =2.727\) in both representations. Using a formula, the equality between the two ways of computing the mean is given in terms of the equation:
\[\bar x = \frac{\sum_{i=1}^n x_i}{n} = \sum_x \big(x \times (f_x/n)\big)\;.\] In the first representation of the arithmetic mean, the average is computed by the summation of all data points and dividing the sum by the sample size. In the second representation, that uses a weighted sum, the sum extends over all the unique values that appear in the data. For each unique value the value is multiplied by the relative frequency of the value in the data. These multiplications are summed up to produce the mean.
The expectation of a random variable is computed in the spirit of the second formulation. The expectation of a random variable is marked with the letter “\(\Expec\)” and is define via the equation:
\[\Expec(X) = \sum_x \big(x \times \Prob(x)\big)\;.\] In this definition all the unique values of the sample space are considered. For each value a product of the value and the probability of the value is taken. The expectation is obtained by the summation of all these products. In this definition the probability \(\Prob(x)\) replaces the relative frequency \(f_x/n\) but otherwise, the definition of the expectation and the second formulation of the mean are identical to each other.
Consider the random variable \(X\) with distribution that is described in Table 4.1. In order to obtain its expectation we multiply each value in the sample space by the probability of the value. Summation of the products produces the expectation (see Table 4.1:
\[\Expec(X) = 0 \times 0.5 + 1 \times 0.25 + 2 \times 0.15 + 3\times 0.10 = 0.85\;.\]
| Value | Probability | Value * Probability |
|---|---|---|
| 0 | 0.50 | 0.00 |
| 1 | 0.25 | 0.25 |
| 2 | 0.15 | 0.30 |
| 3 | 0.10 | 0.30 |
## Expectation = sum(Value*Probability) = 0.85In the example of height we get that the expectation is equal to 170.035 centimeter. Notice that this expectation is equal to \(\mu\), the mean of the population9. This is no accident. The expectation of a potential measurement of a randomly selected subject from a population is equal to the average of the measurement across all subjects.
The sample variance (\(s^2\)) is obtained as the sum of the squared deviations from the average, divided by the sample size (\(n\)) minus 1:
\[s^2 = \frac{\sum_{i=1}^n (x_i - \bar x)^2}{n-1}\;.\] A second formulation for the computation of the same quantity is via the use of relative frequencies. The formula for the sample variance takes the form
\[s^2 = \frac{n}{n-1}\sum_x \big((x - \bar x)^2\times (f_x/n)\big)\;.\] In this formulation one considers each of the unique value that are present in the data. For each value the deviation between the value and the average is computed. These deviations are then squared and multiplied by the relative frequency. The products are summed up. Finally, the sum is multiplied by the ratio between the sample size \(n\) and \(n-1\) in order to correct for the fact that in the sample variance the sum of squared deviations is divided by the sample size minus 1 and not by the sample size.
In a similar way, the variance of a random variable may be defined via the probability of the values that make the sample space. For each such value one computes the deviation from the expectation. This deviation is then squared and multiplied by the probability of the value. The multiplications are summed up in order to produce the variance:
\[\Var(X) = \sum_x\big( (x-\Expec(X))^2 \times \Prob(x)\big)\;.\] Notice that the formula for the computation of the variance of a random variable is very similar to the second formulation for the computation of the sample variance. Essentially, the mean of the data is replaced by the expectation of the random variable and the relative frequency of a value is replaced by the probability of the value. Another difference is that the correction factor is not used for the variance of a random variable.
| \(x\) | \(P(X=x)\) | \(x - E[X]\) | \((x - E[X])^2\) | \(P(X=x)*(x - E[X])^2\) |
|---|---|---|---|---|
| 0 | 0.50 | -0.85 | 0.7225 | 0.361250 |
| 1 | 0.25 | 0.15 | 0.0225 | 0.005625 |
| 2 | 0.15 | 1.15 | 1.3225 | 0.198375 |
| 3 | 0.10 | 2.15 | 4.6225 | 0.462250 |
## Var = sum(p*(x-sum(p*x))^2) = 1.0275As an example consider the variance of the random variable \(X\). The computation of the variance of this random variable is carried out in Table 4.3. The sample space, the values that the random variable may obtain, are given in the first column and the probabilities of the values are given in the second column. In the third column the deviation of the value from the expectation \(\Expec(X) = 0.85\) is computed for each value. The 4th column contains the square of these deviations and the 5th and last column involves the product of the square deviations and the probabilities. The variance is obtained by summing up the products in the last column. In the given example:
\[\begin{aligned} \Var(X) = & (0-0.85)^2 \times 0.5 + (1-0.85)^2 \times 0.25 \\ &+ (2-0.85)^2\times 0.15 + (3-0.85)^2\times 0.10= 1.0275\;.\end{aligned}\]
The standard deviation of a random variable is the square root of the variance. The standard deviation of \(X\) is \(\sqrt{\Var(X)} = \sqrt{1.0275} = 1.013657\).
In the example that involves the height of a subject selected from the population at random we obtain that the variance is \(126.1576\), equal to the population variance, and the standard deviation is 11.23199, the square root of the variance.
Other characterization of the distribution that were computed for data, such as the median, the quartiles, etc., may also be defined for random variables.
4.5 Probability and Statistics
Modern science may be characterized by a systematic collection of empirical measurements and the attempt to model laws of nature using mathematical language. The drive to deliver better measurements led to the development of more accurate and more sensitive measurement tools. Nonetheless, at some point it became apparent that measurements may not be perfectly reproducible and any repeated measurement of presumably the exact same phenomena will typically produce variability in the outcomes. On the other hand, scientists also found that there are general laws that govern this variability in repetitions. For example, it was discovered that the average of several independent repeats of the measurement is less variable and more reproducible than each of the single measurements themselves.
Probability was first introduced as a branch of mathematics in the investigation of uncertainty associated with gambling and games of chance. During the early 19th century probability began to be used in order to model variability in measurements. This application of probability turned out to be very successful. Indeed, one of the major achievements of probability was the development of the mathematical theory that explains the phenomena of reduced variability that is observed when averages are used instead of single measurements. In Chapter 7 we discuss the conclusions of this theory.
Statistics study method for inference based on data. Probability serves as the mathematical foundation for the development of statistical theory. In this chapter we introduced the probabilistic concept of a random variable. This concept is key for understanding statistics. In the rest of Part I of this book we discuss the probability theory that is used for statistical inference. Statistical inference itself is discussed in Part II of the book.
4.6 Exercises
| Value | Probability |
|---|---|
| 0 | 1p |
| 1 | 2p |
| 2 | 3p |
| 3 | 4p |
| 4 | 5p |
| 5 | 6p |
Exercise 4.1 Table 4.4 presents the probabilities of the random variable \(Y\).
These probabilities are a function of the number \(p\), the probability of the value “0”. Answer the following questions:
What is the value of \(p\)?
\(\Prob(Y <3 )\) = ?
\(\Prob(Y = \mbox{odd})\) = ?
\(\Prob(1 \leq Y < 4)\) = ?
\(\Prob(|Y -3| < 1.5)\) = ?
\(\Expec(Y)\) = ?
\(\Var(Y)\) = ?
- What is the standard deviation of \(Y\).
Exercise 4.2 One invests $2 to participate in a game of chance. In this game a coin is tossed three times. If all tosses end up “Head” then the player wins $10. Otherwise, the player losses the investment.
What is the probability of winning the game?
What is the probability of loosing the game?
- What is the expected gain for the player that plays this game? (Notice that the expectation can obtain a negative value.)
4.7 Summary
Glossary
- Random Variable:
The probabilistic model for the value of a measurement, before the measurement is taken.
- Sample Space:
The set of all values a random variable may obtain.
- Probability:
A number between 0 and 1 which is assigned to a subset of the sample space. This number indicates the likelihood of the random variable obtaining a value in that subset.
- Expectation:
The central value for a random variable. The expectation of the random variable \(X\) is marked by \(\Expec(X)\).
- Variance:
The (squared) spread of a random variable. The variance of the random variable \(X\) is marked by \(\Var(X)\). The standard deviation is the square root of the variance.
Discussion in the Forum
Random variables are used to model situations in which the outcome, before the fact, is uncertain. One component in the model is the sample space. The sample space is the list of all possible outcomes. It includes the outcome that took place, but also all other outcomes that could have taken place but never did materialize. The rationale behind the consideration of the sample space is the intention to put the outcome that took place in context. What do you think of this rationale?
When forming your answer to this question you may give an example of a situation from you own field of interest for which a random variable can serve as a model. Identify the sample space for that random variable and discuss the importance (or lack thereof) of the correct identification of the sample space.
For example, consider a factory that produces car parts that are sold to car makers. The role of the QA personnel in the factory is to validate the quality of each batch of parts before the shipment to the client.
To achieve that, a sample of parts may be subject to a battery of quality test. Say that 20 parts are selected to the sample. The number of those among them that will not pass the quality testing may be modeled as a random variable. The sample space for this random variable may be any of the numbers 0, 1, 2, …, 20.
The number 0 corresponds to the situation where all parts in the sample passed the quality testing. The number 1 corresponds to the case where 1 part did not pass and the other 19 did. The number 2 describes the case where 2 of the 20 did not pass and 18 did pass, etc.
Summary of Formulas
- Population Size:
\(N\) = the number of people, things, etc. in the population.
- Population Average:
\(\mu = (1/N)\sum_{i=1}^N x_i\)
- Expectation of a Random Variable:
\(\Expec(X) = \sum_x \big(x \times \Prob(x)\big)\)
- Population Variance:
\(\sigma^2 = (1/N)\sum_{i=1}^N (x_i-\mu)^2\)
- Variance of a Random Variable:
\(\Var(X) = \sum_x\big( (x-\Expec(X))^2 \times \Prob(x)\big)\)
Such a bar plot can be produced with the expression “
plot(table(pop.1$height))”.↩Observe that the function “
var” computes the sample variance. Consequently, the sum of squares is divided by \(N-1\). We can correct that when computing the population variance by multiplying the result by \(N-1\) and dividing by \(N\). Notice that the difference between the two quantities is negligible for a large population. Henceforth we will use the functions “var” and “sd” to compute the variance and standard deviations of populations without the application of the correction.↩The expression \(\{|X -170| \leq 10\}\) reads as “the absolute value of the difference between \(X\) and 170 is no more that 10”. In other words, \(\{-10 \leq X - 170 \leq 10\}\), which is equivalent to the statement that \(\{160 \leq X \leq 180\}\). It follows that \(\Prob(|X-170|\leq 10) = \Prob(160\leq X \leq 180)\).↩
The mean of the population can be computed with the expression “
mean(pop.1$height)”↩